State space in games
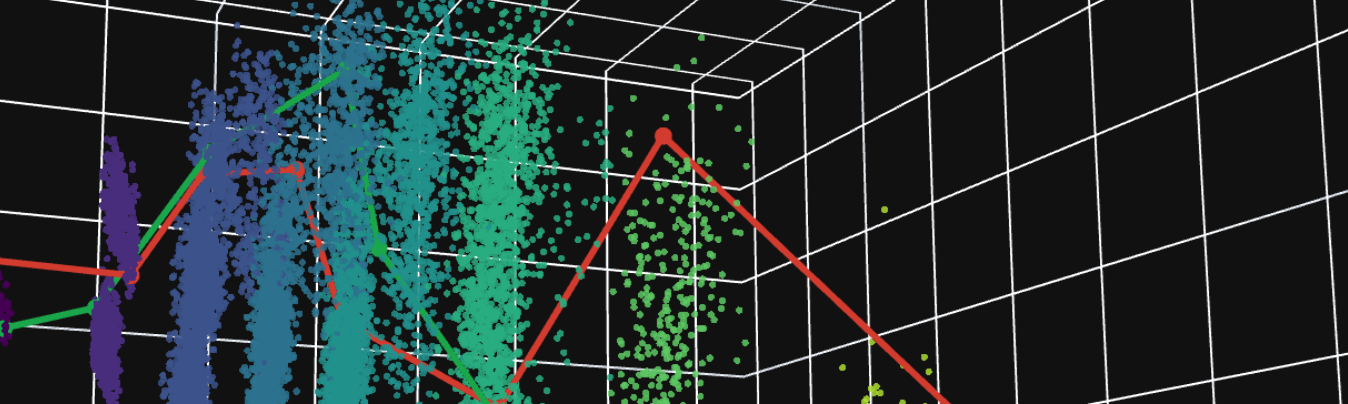
This is a small detour from the L’oaf AI training write-up from a few days ago. I was thinking about if you could represent the game as a set of game-states in a larger, high-dimensional state space. Then we can see what the agent is actually doing in this state-space. I figured I wouldn't learn too much from this, except for getting some nice visuals. To make that map, I generated a big pile of real positions by simulating games between my PPO model and the distilled tree. For each decision point I stored the model’s internal representation of the state, plus metadata like whose outcome it ended up being and which turn it came from. Then I compressed the representation down to 3 dimensions with PCA so it became something I could look at in a 3D graph. On top of this, I showed two trajectories, one in which the AI wins and one in which it loses, to see how the games actually move through the state space. I put the 3D representation below so you can appreciate what it looks like.
What are you looking at? (expand)
- Depth (turn index): which decision number this state is within the game.
- Outcome: final result from p0’s perspective (+1 p0 win, -1 p0 loss).
- kNN value: a smoothed estimate of expected outcome around each point, computed by taking the average outcome of the k nearest neighbors in the plotted embedding (k=300).
- Rep0 / Rep1: the reputation of player 0 and player 1.
- Rep diff (rep0 - rep1): a single axis that compares those two components.
What kNN is doing
kNN smoothing assumes that points that are close in the plotted coordinates are similar game states, and that similar states should have similar outcomes on average. I use the kNN value as a denoiser that highlights broad patches. A large k (300) makes it stable and smooth, and it also blurs boundaries.
The nice surprise is that the cloud does not look like one blob once you see it in 3D. It splits into these repeated sheets that line up cleanly with depth (or: turn index), so the main structure of the space is basically game progression, which feels logical. Within each sheet, the kNN value coloring forms smoother patches. That is a local estimate of how good positions around here tend to be for p0, computed by averaging outcomes of nearby points in the embedded space. It does not give crisp separations, but we can already see that after a few turns the game is starting to split up and who wins is already getting determined.
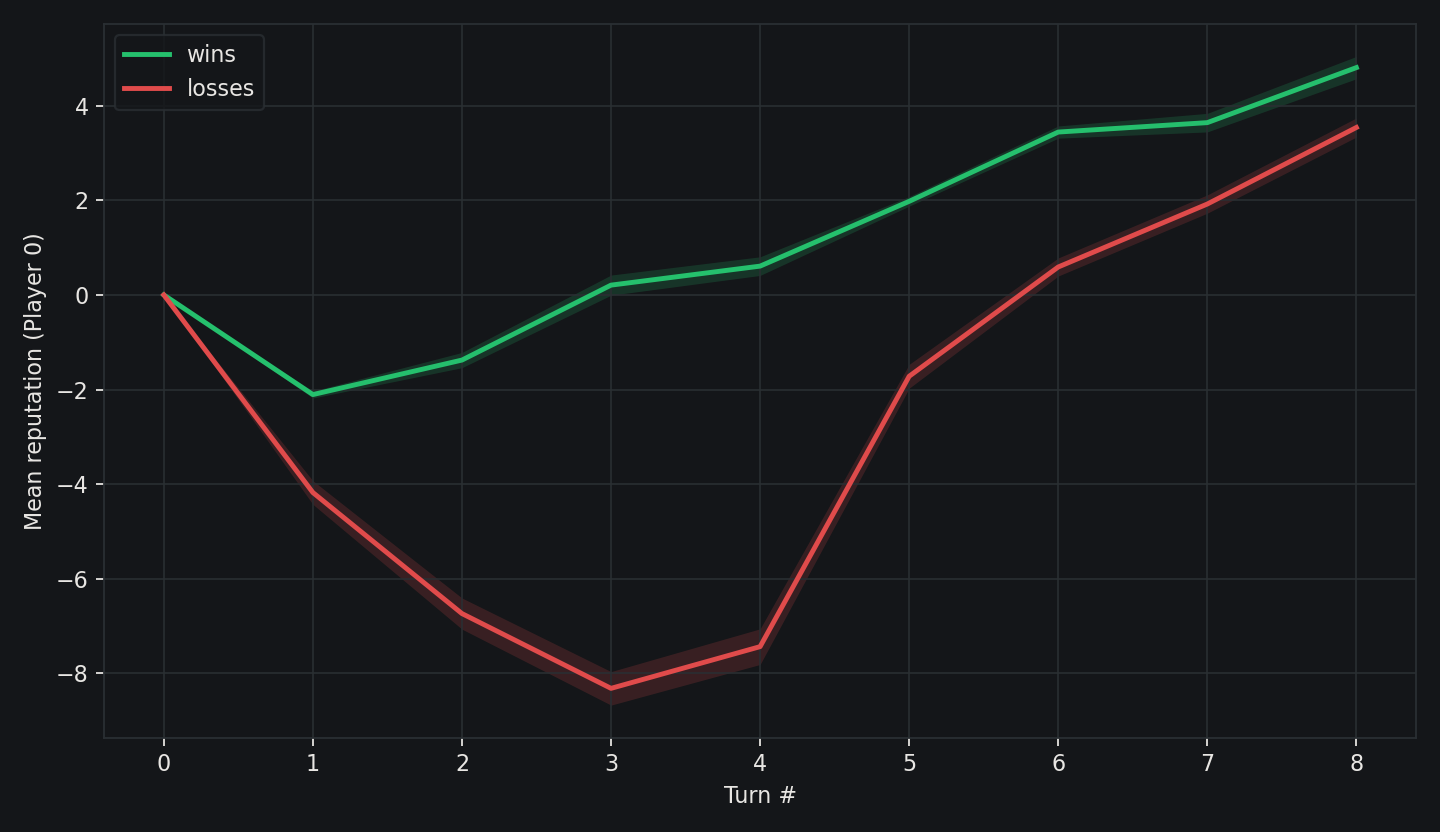
An interesting thing we can do is look at the mean reputation of the stronger player (p0) as turns go on. This of course doesn't require the higher state space, but I thought it was interesting. In wins, the bot usually sacrifices the first round, but not too much. It then on average has a relatively straight path to victory. In losses, it can't quite catch up at the end, but it still ends with a positive reputation. This is of course again not immediately a strategy you should use - it could just be a side effect of the AI playing versus the distilled model, and what tends to work specifically there.
Unfortunately, I do not think this state-space representation gives useful strategy. Much like in biology, a PCA alone isn't really help explain the inner workings of what you're looking at, but it feels like a useful view. You probably need to do mechanistic modeling or something similar to really understand what is happening.





